MAA11 Algoritmit ja lukuteoria

Jaollisuus ja alkuluvut

Eukleideen algoritmi

Eukleideen algoritmi ratkaisee kahden positiivisen kokonaisluvun suurimman yhteisen tekijän. Algoritmi perustuu tulokseen, jonka mukaan jakoyhtälössä \[a = qb + r\] lukujen $a$ ja $b$ yhteiset tekijät ovat samat kuin lukujen $b$ ja $r$ yhteiset tekijät. Lukujen $b$ ja $r$ jakoyhtälöstä päästään yhä pienempiin lukuihin, ja vastaus on selvillä, kun jako menee tasan. Esimerkiksi \[\textrm{syt}(33, 27) = \textrm{syt}(27, 6)=\textrm{syt}(6, 3) = 3, \] sillä

• $33 = 1\cdot 27 + 6 $,
• $27 = 4\cdot 6 + 3$ ja
• $6 = 2\cdot 3 + 0$.

Viimeinen jakaja $3$ on suurin yhteinen tekijä. Prosessia voi havainnollistaa myös seuraavasti:

---

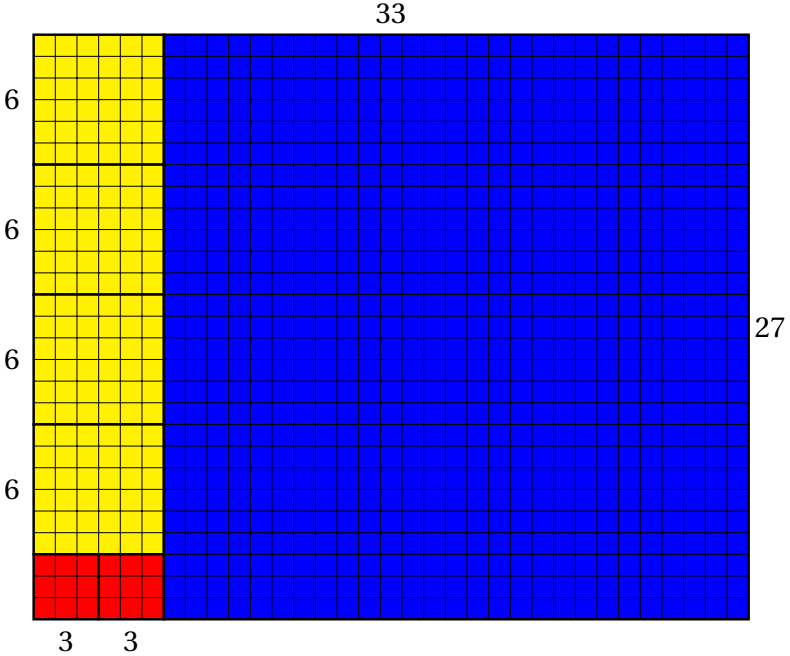
Tehtävä 1 Ratkaisematon

Kirjoita ohjelma, joka laskee lukujen 210592578 ja 120065279 suurimman yhteisen tekijän Eukleideen algoritmilla. Jakojäännös on mukavinta laskea operaattorilla %. Ohjelman tulee tulostaa vain vastaus.

Kirjoita ohjelma tähän:

---

Alkulukutestaus

Alkuluku on lukua $1$ suurempi kokonaisluku, joka on jaollinen vain itsellään ja luvulla $1$. Esimerkiksi seuraavalla funktiolla voi testata, onko kyseessä alkuluku. Algoritmin idea on testata luvun $n$ jaollisuutta yrittämällä jakaa se vuorollaan kaikilla luvuilla $2$, $3$, ... $n-1$. Tämä algoritmi on hyvin hidas.

def onko_alkuluku(luku): 
    if luku < 2: 
        return False
    
    for jakaja in range(2, luku):
        if luku % jakaja == 0:
            return False
    
    return True
    
print(onko_alkuluku(137))

Tulostus:

True

Edellä esitetyn algoritmin nopeutta voi testata käyttämällä moduulin time funktiota time. Valitaan sopivan suuri alkuluku ja testataan:

from time import time

def onko_alkuluku(luku): 
    if luku < 2: 
        return False
    
    for jakaja in range(2, luku):
        if luku % jakaja == 0:
            return False
    
    return True

n = 30000001

alkuaika = time()
print(onko_alkuluku(n))
loppuaika = time()

print("Aikaa kului sekunteina:")
print(loppuaika-alkuaika)

Tämän ohjelman suoritus kestää kauan.

---

Tehtävä 2 Ratkaisematon

Edellisen esimerkin algoritmia voi parantaa varsin yksinkertaisesti. Jos luvulla on tekijöitä, ne esiintyvät parettain: Esimerkiksi \[36 = 2\cdot 18= 3\cdot 12 = 4\cdot 9 = 6\cdot 6.\] Jos kaksi tekijää ovat yhtä suuret, ne ovat kyseisen luvun neliöjuuria ($\sqrt{36}=6$). Muussa tapauksessa toinen tekijä on neliöjuurta pienempi ja toinen suurempi.

Tästä seuraa, että jos luku $n$ ei ole alkuku, sillä on ykköstä suurempi tekijä, jonka suuruus on korkeintaan $\sqrt{n}$. Alkulukutestauksessa riittää siis siis tarkistaa jakajat $2$, $3$, ..., $\sqrt{n}$.

Kopioi edellisen esimerkin koodi ja paranna onko_alkuluku-funktiota edellä mainitulla tavalla. Jätä ohjelman tulosteet samanlaisiksi kuin esimerkissä. Neliöjuurikomento sqrt löytyy math-moduulista. Voit pyöristää neliöjuuren tuloksen alaspäin kokonaisluvuksi funktiolla int.

Kirjoita ohjelma tähän:

---

Eratostheneen seula

Eratostheneen seula pitää yllä kirjanpitoa, jossa on luvut 2...n. Algoritmi käy läpi luvut pienimmästä suurimpaan. Jokaisen luvun i kohdalla algoritmi merkitsee rastin luvun moninkertojen 2*i, 3*i, 4*i jne. kohdalle. Rasti tarkoittaa, että kyseinen luku ei ole alkuluku, koska se on jaollinen luvulla i. Kun algoritmi päättyy, alkuluvut tunnistaa siitä, että niiden kohdalla ei ole rastia.

Tarkastellaan esimerkkinä Eratostheneen seulan toimintaa, kun n on 100. Tällöin algoritmi etsii kaikki alkuluvut, jotka ovat välillä 2...100. Tässä on algoritmin aloitustilanne:

Algoritmi rastittaa ensin luvun 2 moninkerrat 4, 6, 8, jne.:

Sitten algoritmi rastittaa luvun 3 moninkerrat 6, 9, 12, jne.:

Algoritmi jatkaa vastaavalla tavalla eteenpäin, kunnes se on käynyt läpi kaikki välin 2...100 luvut. Tällöin kirjanpidon sisältö on seuraava:

Tämä tarkoittaa, että alkuluvut välillä 2...100 ovat:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Seulan toteutus

Jotta voimme ohjelmoida Eratostheneen seulan, tarvitsemme keinon pitää muistissa lukujen kirjanpitoa. Hyvä tapa tähän on luoda lista, jossa on kohta jokaiselle kirjanpidon luvulle. Voimme luoda listan näin:

seula = [0]*(n+1)

Tämän listan kohdat on numeroitu 0, 1, 2, ..., n, ja jokaisessa kohdassa on aluksi luku 0. Ideana on, että kohdassa seula[x] on tieto, onko luku x rastitettu. Arvo 0 tarkoittaa, että lukua ei ole rastitettu, ja arvo 1 tarkoittaa, että luku on rastitettu. Huomaa, että emme käytä listan kohtia 0 ja 1 algoritmin aikana, koska tarvitsemme kirjanpitoa vasta kohdasta 2 alkaen.

Seuraava koodi toteuttaa Eratostheneen seulan:

n = 100
seula = [0]*(n+1)
for i in range(2,n+1):
    for j in range(2*i,n+1,i):
        seula[j] = 1

Koodin pääsilmukka käy läpi luvut 2...n, ja kunkin luvun i kohdalla sisäsilmukka merkitsee, että luvun moninkerrat 2*i, 3*i, 4*i, jne. eivät ole alkulukuja.

Tämän jälkeen voimme tulostaa löytyneet alkuluvut näin:

for i in range(2,n+1):
    if seula[i] == 0:
        print(i)

Esimerkiksi kun n on 100, koodin tulostus on seuraava:

2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97

---

Tehtävä 3 Ratkaisematon

Välillä 1...100 on 25 alkulukua. Montako alkulukua on välillä 1...1000?

Kirjoita ohjelma tähän:

---

Tehtävä 4 Ratkaisematon

Välin 1...100 alkulukujen summa on 1060. Mikä on välin 1...1000 alkulukujen summa?

Kirjoita ohjelma tähän:

---

Tehtävä 5 Ratkaisematon

Alkulukupari muodostuu kahdesta alkuluvusta, joiden ero on 2. Välillä 1...100 on seuraavat alkulukuparit:

3 5
5 7
11 13
17 19
29 31
41 43
59 61
71 73

Tee ohjelma, joka tulostaa vastaavalla tavalla välin 1...1000 alkulukuparit.

Kirjoita ohjelma tähän:

---